ORDONNÉS (ENSEMBLES)

ORDONNÉS (ENSEMBLES)

Les relations d’ordre interviennent de manière naturelle dans des questions comme l’étude des liens de parenté et celle des liens de subordination, comme les problèmes de classification, etc. C’est de là, et de la relation 諒 entre nombres, que découle la terminologie habituellement employée: on dit que a est «plus petit» que b , que a est «dominé» par b , que b est «plus haut» que a , etc. Remarquons que cette situation inclut l’égalité a = b ; on précise que, de plus, a b , en ajoutant l’adverbe «strictement».

La théorie des ensembles ordonnés comporte une partie élémentaire qui est exposée ici, mais constitue aussi un chapitre important de la «grande» théorie des ensembles (cf. LOGIQUE MATHÉMATIQUE - Théorie axiomatique des ensembles) en liaison étroite avec l’axiome du choix dont plusieurs formulations équivalentes s’expriment en terme d’ordre. La théorie des ordinaux, due à Cantor, s’exprime aussi dans ce cadre. Rappelons enfin que c’est à partir de la relation d’ordre usuel sur l’ensemble des nombres rationnels que R. Dedekind, en 1872, a donné la première construction rigoureuse de l’ensemble des nombres réels (cf. nombres RÉELS).

Relations d’ordre

On dit qu’une relation 倫 sur un ensemble E est une relation d’ordre (cf. théorie élémentaire des ENSEMBLES, chap. 2) si elle satisfait aux axiomes suivants:

(O¹) Réflexivité: pour tout élément a de E, on a la relation a 倫a ;

(O²) Antisymétrie: les relations a 倫b et b 倫a ne sont compatibles que pour a = b ;

(O³) Transitivité: les relations a 倫b et b 倫c impliquent a 倫c .

Par exemple, la relation 諒 est une relation d’ordre sur tout sous-ensemble de l’ensemble R des nombres réels.

Étant donné deux nombres réels distincts a et b , on a toujours une, et une seule, des relations a 諒 b ou b 諒 a . Plus généralement, si E est un ensemble muni d’une relation d’ordre 倫, on dira que deux éléments a et b sont comparables si on a au moins une des relations a 倫b ou b 倫a . Si deux éléments quelconques d’un ensemble ordonné E sont toujours comparables, on dit que E est totalement ordonné, ou encore que l’ordre est total , ou linéaire. Dans le cas contraire, on parle d’ordre partiel .

Un exemple d’ordre partiel

Soit X un ensemble; la relation d’inclusion 說 est une relation d’ordre sur l’ensemble E = 戮(X) des parties de X (cf. théorie élémentaire des ENSEMBLES, chap. 1). Sur la figure 1, on a représenté le diagramme sagittal de cette relation dans le cas où X = 見, 廓, 塚 est un ensemble à trois éléments: pour a, b 捻 戮(X), on a:

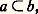si a = b ou s’il existe une ou plusieurs flèches «consécutives» du diagramme partant de a pour aboutir à b. Les parties 廓 et 見, 塚, par exemple, ne sont pas comparables et l’ordre n’est donc pas total.

Intervalles

Soit E un ensemble ordonné et a et b des éléments de E avec a plus petit que b. On appelle intervalle ouvert d’origine a et d’extrémité b , noté ]a b [, l’ensemble des éléments x de E qui sont strictement plus grands que a et strictement plus petits que b (donc en particulier comparables à a et à b ). Ainsi on a, dans l’exemple précédent illustré par le diagramme de la figure 1,

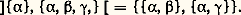On définit de même, pour a plus petit que b , l’intervalle fermé [a , b ] qui est l’ensemble des éléments x de E qui sont plus grands que a et plus petits que b : c’est l’intervalle ouvert ]a , b [ augmenté de ses deux extrémités.

Majorants

Soit E un ensemble ordonné et A un sous-ensemble de E. On dit qu’un élément m de E est un majorant de A si tout élément de A est plus petit que m (ce qui implique que tout élément de A est comparable à m ); si A admet au moins un majorant, on dit que c’est un ensemble majoré. Dans le cas où, de plus, m appartient à A, on dit que A admet un plus grand élément; il résulte de (O²) que ce plus grand élément m , s’il existe, est unique.

Reprenons encore l’exemple ci-dessus, illustré par le diagramme de la figure 1, avec:

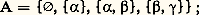cet ensemble admet pour majorant m = 見, 廓, 塚, mais n’admet pas de plus grand élément. L’élément 廓, 塚 de A n’est pas un plus grand élément (car il n’est pas comparable à 見, 廓), mais possède la propriété plus faible qu’il n’existe pas d’élément de A qui soit strictement plus grand que lui: on dit que c’est un élément maximal .

Borne supérieure

Soit toujours E un ensemble ordonné et A un sous-ensemble de E que nous supposerons majoré. Tout élément de E plus grand qu’un majorant de A est a fortiori un majorant de A et il est donc intéressant de chercher des majorants le plus petits possible. On dit que A admet une borne supérieure si l’ensemble de ses majorants a un plus petit élément; cet élément, nécessairement unique, s’appelle la borne supérieure de A et on le note:

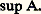Bien entendu, on définirait de même la notion de borne inférieure.

Dans le cas des nombres réels, tout ensemble majoré admet une borne supérieure (cf. CALCUL INFINITÉSIMAL - Calcul à une variable, chap. 1) et c’est cette importante propriété qui permet de «faire de l’analyse», alors que l’existence de lacunes dans l’ensemble des nombres rationnels met cette propriété en défaut: c’est ainsi que l’ensemble des nombres rationnels dont le carré est strictement inférieur à 2 n’admet pas de borne supérieure dans Q; dans R, sa borne supérieure est le nombre (irrationnel) 連

Lorsque l’ordre est total, tout sous-ensemble fini a un plus grand élément; mais il n’en est plus de même si l’ordre est partiel. Étant donné deux éléments a et b , on désigne par:

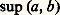la borne supérieure (si elle existe) de l’ensemblea , b. Par exemple, si l’ensemble E = 戮(X) des parties d’un ensemble X est ordonné par inclusion, soit a et b deux parties de E. Une partie c est «plus grande» que a et que b , c’est-à-dire a 說 c et b 說 c , si, et seulement si, a 聆 b 說 c ; la réunion a 聆 b est donc le plus petit majorant commun à a et à b , c’est-à-dire la borne supérieure. Raisonnant de même pour la borne inférieure, on a donc dans notre exemple:

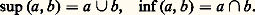On appelle treillis tout ensemble ordonné dans lequel deux éléments quelconques ont toujours une borne supérieure et une borne inférieure; la théorie des treillis est une branche de l’algèbre qui a de nombreuses applications tant en mathématiques pures qu’en mathématiques appliquées.

Quelques ordres sur N

On peut munir l’ensemble N des entiers naturels strictement positifs de diverses relations d’ordre qui montreront bien la grande variété de propriétés que l’on peut obtenir ainsi.

Après la relation 諒 usuelle, la relation d’ordre la plus courante est la relation de divisibilité:

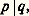si p divise q , c’est-à-dire si q est multiple de p : cela signifie qu’il existe un entier m 捻 N tel que q = mp. Sur la figure 2, on a représenté le diagramme sagittal de l’ordre ainsi obtenu sur l’ensemble des huit multiples du nombre 30. On remarque la parfaite analogie avec l’ensemble des parties de X = 見, 廓, 塚 ordonné par inclusion ; plus généralement, on dit que deux ensembles ordonnés sont isomorphes s’il existe une bijection de l’un sur l’autre qui respecte les ordres.

La relation de divisibilité ne définit pas un ordre total, car 2 et 3, par exemple, ne sont pas comparables. Si p et q sont deux entiers, l’ensemble des «majorants» communs est l’ensemble des multiples communs de p et de q ; cet ensemble a un «plus petit» élément, le plus petit commun multiple (P. P. C. M.) de p et de q , qui est donc la borne supérieure de p et de q pour la relation de divisibilité. On interpréterait de même le P. G. C. D. (plus grand commun diviseur) de p et de q comme la borne inférieure de p et de q , ce qui donne une structure de treillis.

Très différente est la relation d’ordre suivante sur N, qui intervient dans une démonstration du théorème de d’Alembert sur les racines d’une équation algébrique. On remarque d’abord que tout entier n 閭 1 s’écrit de manière unique sous la forme:

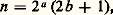avec a , b 捻 N. Cela signifie que n est divisible par 2^a , mais pas par 2^{a +1}; le quotient de n par 2^a est alors un entier impair, donc de la forme 2b + 1. Par exemple, 72 est divisible par 8 = 2³ mais n’est pas divisible par 16 = 2⁴; le quotient de 72 par 8 est le nombre impair 9 = 4 憐 2 + 1, d’où l’on a 72 = 2³(4 憐 2 + 1).

Pour n = 2^a (2b + 1) et n = 2^a (2b + 1), on dira que n est dominé par n , et on notera n 諒 n , si on a:

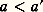ou si on a simultanément:

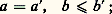on définit ainsi une relation d’ordre total très différente de l’ordre usuel. Par exemple 31 諒 2 ou 12 諒 8. L’intervalle ouvert ]2, 14[ contient les nombres 6 et 10, mais l’intervalle ]2, 12[ contient une infinité d’éléments, à savoir tous les nombres de la forme 2(2 k + 1), k 閭 1, et le nombre 4 qui est son plus grand élément.

L’ordre lexicographique

Un ordre important dans les applications les plus variées (pour tous les problèmes de classification en sciences humaines, par exemple) est l’ordre lexicographique. Il est familier à tous ceux qui ont consulté un dictionnaire.

Soit X un ensemble ordonné par 諒 que nous appellerons un alphabet. On appelle mot toute suite finie d’éléments de X, sans se préoccuper du sens éventuel de ce mot dans une langue naturelle. Par exemple, si X est l’alphabet usuel, constitué par nos vingt-six lettres,

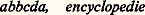sont des mots.

L’ordre lexicographique se définit alors sur l’ensemble E des mots de la manière suivante. Si x = x ¹x ² ... x ^p et y = y ¹y ² ... y ^q sont des mots, on dira que:

si on a p 諒 q et x ¹ = y ¹, x ² = y ², ..., x ^p = y ^p , ou si, désignant par k le plus petit entier tel que x ^k y ^k , on a x ^k 諒 y ^k . Ainsi, si l’un des deux mots n’est pas obtenu en rajoutant des lettres à l’autre, on classe ces mots en examinant la première lettre qui diffère, par exemple: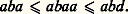

Encyclopédie Universelle. 2012.